A continuación les presentamos el tercer artículo de Vinicio Vásquez Bernal, relacionado con su investigación sobre la Taptana, la Calculadora de los Cañarís. Hoy se referirá al algoritmo de la sustracción.
Sustraer representa quitar una cantidad de otra, la Taptana es de gran ayuda y permite operar de manera muy práctica para realizar este cálculo. Está claro que nos sujetaremos a las normas generales y en ese contexto se propondrá un algoritmo para esta operación.
Para la explicación de este algoritmo, llamaremos minuendo a la cantidad inicial, y sustraendo a la cantidad que vamos a retirar de la definida anteriormente. Por supuesto que debe cumplirse que el minuendo debe ser mayor o igual al sustraendo, si esto se ratifica entonces puedo iniciar el algoritmo. En primer lugar, se ubicará la cantidad del minuendo en la Taptana, y la cantidad del sustraendo fuera de la calculadora, teniendo claro la simbología expuesta para los distintos elementos y su relación de correspondencia con las columnas del utensilio. La operación se realizará columna a columna, iniciando por la izquierda; es decir, arrancaremos por la columna de las unidades, y para los elementos correspondientes a cada columna realizaremos el siguiente proceso:
Comparamos la cantidad de elementos presentes en la columna del minuendo con la cantidad de elementos presentes en la respectiva columna del sustraendo, pudiendo darse los siguientes casos:
1.- Si los del minuendo son más que los del sustraendo, simplemente de la columna de la Taptana retiro tantos elementos como los que existan en el sustraendo, iniciando desde arriba.
2.- Si los del minuendo son igual en cantidad a los del sustraendo, retiro todos los elementos de esa columna de la Taptana.
3.- Si los del minuendo son menos que los del sustraendo:
I. Retiro de la respectiva columna de la Taptana, todos los elementos presentes y del sustraendo una cantidad equivalente.
II. Cambio un elemento de la columna inmediatamente anterior derecha de la taptana por una columna llena y un elemento en la concavidad mayor.
III. Retiro de la Taptana la cantidad de elementos igual a los quedaron pendientes, iniciando por el elemento de la concavidad mayor y luego los elementos de la respectiva columna, comenzando desde arriba.
IV. En caso de que en la columna inmediatamente anterior no exista elemento alguna, recurriremos a la siguiente que tenga elementos y esté ubicada lo más próxima a la derecha, transformando un elemento de ésta en una columna llena y un elemento en la concavidad grande, para luego transformar este elemento de la concavidad grande en una columna llena más un elemento de esas características en la concavidad grande, procedimiento que puede repetirse tantas veces sea necesario.
V. En vista de que al inicio nos aseguramos que el minuendo sea mayor o igual al sustraendo en la última columna siempre los elementos del minuendo podrán retirarse con los del sustraendo.
Al concluir con la última columna de la derecha, en la Taptana quedará representada la cantidad que corresponde al resultado de la sustracción.
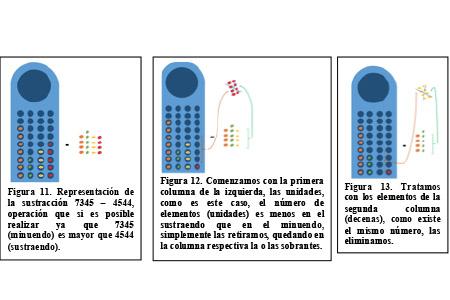
EJEMPLO: Realizaremos la siguiente sustracción 7345-4544, En primer lugar, ubicamos minuendo y sustraendo, el primero dentro de la Taptana y el segundo fuera de la misma, tal como se observa en la figura 11. Iniciamos la operación con la columna de la derecha que corresponde a unidades, en el minuendo existen 5 y en el sustraendo existen 4, eliminamos de estas una cantidad igual de la columna de unidades (figura 12), quedando un elemento en la columna respectiva; luego, para las decenas, la cantidad de elementos en la columna de la Taptana como los que están fuera son iguales (4), eliminamos de ambas, como se muestra en la figura 13 y esa columna de la Taptana queda vacía.
Vemos luego los elementos de las centenas, en la Taptana tenemos 3 y fuera tenemos 5, lo primero que haremos será eliminar esos 3 de la Taptana con cantidad igual de los de fuera, como se observa en la figura 14, quedando al exterior de la maquina 2 elementos sobrantes.Para poder proceder cambiamos un elemento de la columna de la izquierda, en este caso de las unidades de mil, por una columna llena de centenas, más una en la concavidad mayor (en total colocamos diez) lo que se presenta en la figura 15. Este proceso puede ampliarse en caso de que no existan elementos en la columna inmediatamente anterior, en ese caso deberemos proseguir a la columna de la derecha más próxima que sí cuente con elementos, para con uno de ellos realizar el cambio con elementos que llenen la siguiente columna más uno en la concavidad mayor. Luego cambiaremos ese elemento de la concavidad mayor por los elementos que correspondan, así hasta llegar a la columna requerida.
Para continuar retiramos tantas fichas como las que están fuera de la Taptana, iniciando por la que se ha ubicado en la concavidad mayor y luego los de la columna, iniciando desde arriba (figura 16), en este caso retiramos dos. Por último, en la última columna de las unidades de mil, siempre los que están en la columna de la Taptana serán mayor o igual a los que están fuera, esto porque como condición inicial exigimos que el minuendo sea mayor o igual que el sustraendo. Simplemente retiraremos de dicha columna tantos como los que se hallen fuera, en este caso 4, (figura 17).
Una vez concluida con la operación en esta última columna, en la Taptana se representará la cantidad que es el resultado de sustraer 4544 de 7345. En la figura 18 vemos que la cantidad representada es 2801, y efectivamente 7345 – 4544=2801