Por: Vinicio Vásquez Bernal
REPRESENTACIÓN DE UNA CANTIDAD.- Para entender a cabalidad esta representación, una vez que se ha indicado las condiciones y hemos acordado la respectiva simbología, lo que haremos será ubicar en las respectivas columnas de la Taptana, tantos símbolos como la respectiva cantidad de unidades, decenas, centenas y unidades de mil, que estén presentes en la cantidad a requerir lo indiquen.
Se debe recordar que la numeración utilizada por los Cañarís, debió ser auténtica, por lo tanto su simbología debe entenderse de manera autónoma, sin condición de sujetarse a lo que actualmente aceptamos. En este trabajo se explicará con sus respectivas equivalencias únicamente para fines de un entendimiento cabal y para demostrar que estos procesos y algoritmos son absolutamente correctos.
Ejemplos
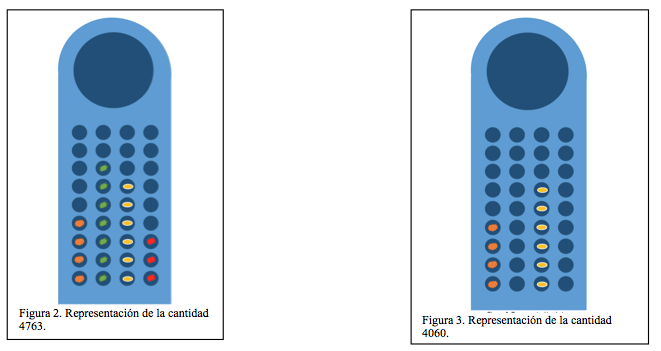
Para representar una cantidad de 4763 elementos, sobre la Taptana ubicaremos los símbolos como se muestra en la Figura 2, donde se observa que se han ubicado 3 unidades, 6 decenas, 7 centenas y 4 unidades de mil.
En cambio, si deseamos representar el 4060, donde se tienen cero unidades y cero centenas, simplemente no se ubicarán símbolos en las respectivas columnas, como se observa en la Figura 3.
Conteo
La operación matemática más común, y quizá la que mayor complejidad guarda es aquella de contar; es decir, ir aumentando una unidad cada vez en la Taptana. Su realización es muy simple, lo que se hace es simplemente ir ubicando un elemento unidad en la misma desde su columna izquierda, que justamente corresponde a las unidades, siempre de abajo hacia arriba, teniendo en cuenta que si dicha columna está llena, se ubicará la nueva unidad en la concavidad mayor, lo que a su vez exigirá un cambio donde se remplazará todos los elementos de la columna y el de igual orden que se encuentra en la concavidad mayor por uno de mayor orden. En realidad, se cambia diez unidades por una decena.
Se presentarán casos donde también la columna de decenas esté llena; en ese caso, el nuevo elemento que surge de cambiar las unidades, se ubicará en la concavidad mayor, lo que a su vez obliga un cambio de toda la segunda columna más el de la concavidad mayor por un nuevo elemento de mayor orden. En este caso una centena, es decir cambiamos diez decenas por una centena. Este caso puede generalizarse para órdenes mayores.
Algoritmo de la adición
 Está herramienta de cálculo permite sumar directamente dos o más cantidades, teniendo en cuenta que su estructura tradicional es de cuatro columnas; es decir, el resultado máximo a obtenerse es 9999.
Está herramienta de cálculo permite sumar directamente dos o más cantidades, teniendo en cuenta que su estructura tradicional es de cuatro columnas; es decir, el resultado máximo a obtenerse es 9999.
Al igual que el proceso mental de sumar varias cantidades, en esta y en todas las máquinas de cálculo, el proceso será sumar dos números y al resultado adicionar las demás. Por lo tanto deberemos exponer el algoritmo para sumar dos números enteros, que según las características de esta máquina, su resultado debe ser menor o igual a 9999
Algoritmo para sumar dos números
1. Representar uno de los números sobre la Taptana, de acuerdo a lo expuesto anteriormente.
2. Ubicar el otro número fuera de la Taptana.
3. Comenzando desde las unidades, es decir de la columna izquierda, se irá añadiendo en las columnas correspondientes los elementos: un elemento por cada concavidad pequeña, si se llena la columna, y existen elementos sobrantes, ubicamos uno en la concavidad grande.
4. Si se ha llenado la columna y está un elemento en la concavidad mayor, se cambiarán estos diez elementos, retirándoles del proceso y ubicando un nuevo elemento correspondiente a los que deben ubicarse en la columna situada a la derecha de la que fue llenada.
5. Si hubieran elementos que luego de llenar la columna respectiva y ubicar un elemento en la concavidad mayor, luego de hacer el cambio expuesto en el paso 4, se colocarán los elementos sobrantes en la correspondiente columna.
Ejemplo
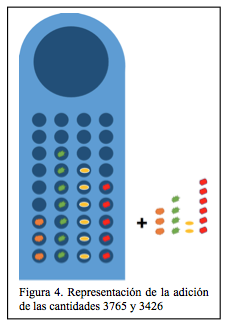
Aquí explicaremos el proceso para adicionar dos números, iniciando con ubicar uno de ellos directamente en la Taptana y el otro fuera de la misma, tal como se observa en la figura 4. En la que representamos la cantidad 3765 en el utensilio y 3426 fuera de este, teniendo en cuenta que en la columna de la izquierda ubicaremos las unidades, luego decenas, centenas y unidades de mil.
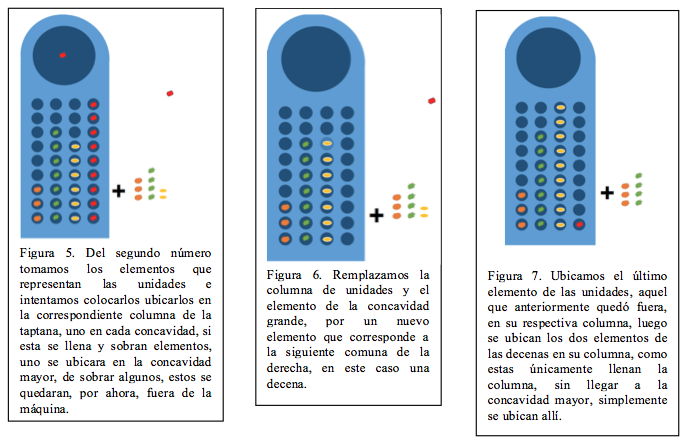
Luego como se observa en la figura 5. Tomamos los elementos unidades de la columna de unidades del segundo número e intentamos ubicarlos en la columna respectiva de unidades, si ubicando uno en cada concavidad pequeña se llena sin sobrar ninguno, los ubicaríamos y listo.Sin embargo, como se ve en este caso, se llena la columna, se ubica otro elemento en la concavidad mayor y aún así sobra un elemento de las unidades que queda fuera de la calculadora.
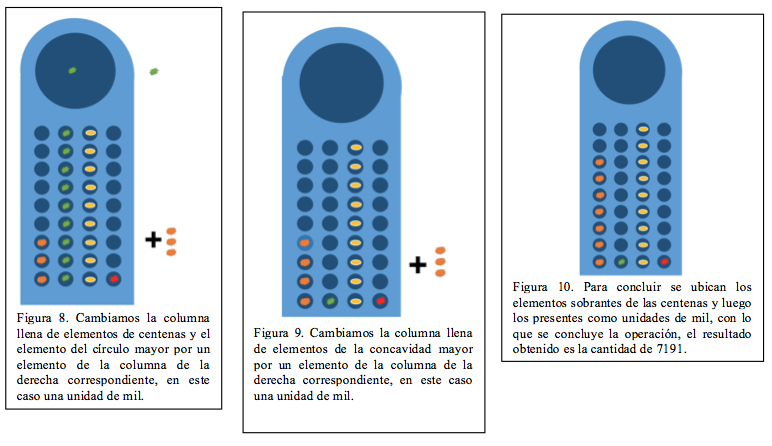
La columna llena junto al elemento ubicado en la concavidad mayor nos indican que tenemos diez unidades, por lo que procedemos a remplazar éstas, vaciando la columna y el elemento de la concavidad mayor y añadiendo un nuevo elemento de decena en la columna respectiva, tal como se observa en la figura 6, recordando que tenemos un elemento de unidades que está fuera de la Taptana, ubicamos este en la columna de unidades que ya se vació y procedemos con los elementos de la siguiente columna, en este caso las decenas. En este caso existen 2 elementos que corresponden a los elementos del segundo número, estos se pueden ubicar en las concavidades pequeñas de la columna de decenas de la calculadora, las ubicamos y listo, tal como se observa en la figura 7. Procedemos luego con los elementos de las centenas del segundo número, aquí nuevamente llenamos la columna, ubicamos uno en la concavidad mayor, y queda uno restante (Figura 8), remplazamos esta columna y la del círculo grande con una unidad de mil (Figura 9). Ingresamos a la Taptana la centena que estaba fuera y por ultimo ingresamos los elementos correspondientes a las unidades de mil del segundo número, obteniendo ya el resultado definitivo.
Debe indicarse que puede darse el caso en alguna parte del proceso de que se llene la columna y además extra un elemento para ubicarse en la concavidad grande, sin quedar elementos respectivos a esa columna fuera de la taptana, simplemente se realizará el remplazo con un elemento en la siguiente columna de la derecha, y como no quedó elemento alguno fuera, la columna en cuestión permanecerá vacía, indicándonos que existen cero elementos, ya sean unidades, decenas, centenas o unidades de mil.
NOTA: La próxima semana indicaremos el algoritmo de la sustracción.
