Por: Vinicio Vásquez Bernal
Presentamos en este espacio los resultados obtenidos en un proyecto investigativo que se ha desarrollado con la ayuda de la Casa de la Cultura Ecuatoriana y alumnos del paralelo 7 de la Universidad Nacional de Educación (UNAE).
La TAPTANA, es un objeto que evidencia la grandiosidad de la Nación Cañarí del que se ha tenido noticias desde inicio de la conquista, del cual se han escrito varios artículos presentándolo como una herramienta de contabilidad o de juegos. Existe, por ejemplo, una explicación notable en el libro “EL AZUAY HISTÓRICO, LOS CAÑARÍS Y LOS INCO CALARIS”, del Doctor Octavio Cordero Palacios, publicado en 1984. Cabe también indicar que en el libro “RECONOCIMIENTO Y EXCAVACIONES EN EL AUSTRO ECUATORIANO” de Donald Collier y Jhon Murra de 1943, la lámina principal se la dedica a la tartana. Mas su abordaje siempre ha sido arqueológico-histórico, sin tomar en cuenta su contribución matemática. En tal virtud no se han presentado los algoritmos que sustenten cómo esa herramienta era utilizada para realizar las operaciones matemáticas: Representación de una cantidad, el proceso de contar, la suma, la diferencia, el producto y la división, mismos que hemos podido descubrir para presentarlos en estas entregas.
Por razones de espacio, hemos resuelto editar en seis partes, para presentarlo en estos espacios, iniciando con una explicación histórica, la estructura, la forma de construir y normas que deberán cumplirse.
Reseña histórica
Me refiero a la TAPTANA, un artefacto, cuya construcción responde a la fidelidad de la cultura Cañarí con su entorno natural. Se han encontrado vestigios en madera y principalmente en piedra. Existen varias referencias de su utilización por los descendientes de la guacamaya, los mismos cronistas que acompañaron la feroz conquista relatan cómo esa “tabla de cálculo y juego” era utilizada por los originarios de esta tierras. A decir de expertos, sus restos nos llevan al periodo Tacalzhapas, es decir unos 500 años antes de Cristo, lo que permite afirmar que al igual que todas las grandes civilizaciones de la humanidad, los Cañarís también entendieron las matemáticas en su fundamento teórico, al grado de ser capaces de construir una máquina de cálculo, y lo hicieron al menos dieciséis siglos antes de aquellos que llegaron como civilizadores, superando también al Quipu de los Incas que únicamente utiliza al número en su acepción de información y no permite operación alguna.
La efectividad de esta herramienta se puede explicar a través de algoritmos simples que permiten la realización correcta de las operaciones aritméticas que además se sujetan a la tangibilidad de la ciencia y la concreción de los conceptos de cantidad, siempre dentro del contexto de la filosofía andina, de la cruz cuadrada, de esas ideas donde el vació no existe y la cantidad son conceptos ligados a los seres supremos.
Construcción
Las taptanas que se han encontrado han sido talladas en piedra o construidas en madera; su estructura es diversa, más siempre sujetándose a dos características esenciales:
1. Una CONCAVIDAD MAYOR, ubicada en la parte más importante del objeto.
2. Varias hileras de nueve CONCAVIDADES MENORES, perfectamente definidas y agrupadas de forma que no generen ambigüedad alguna.
Estas estructuras no responden a dimensiones definidas ni respetan proporcionalidad alguna, simplemente presentan distintas concavidades perfectamente separadas y agrupadas.
En la Figura 1, se presenta la llamada TAPTANA NIKICHIK que consiste en un tipo muy conocido, un rectángulo al que en uno de los lados más pequeños se le ha añadido un semicírculo, y en su interior tiene concavidades circulares, una grande que se conoce como concavidad mayor en la parte del semicírculo y 4 hileras de nueve círculos cada una, conocidos como concavidades menores, estos de menor tamaño. Esta construcción permite albergar cantidades enteras entre 0, incluido, y 10000, no incluido.
Condiciones generales
Para un cabal entendimiento de esta calculadora debemos indicar ciertas cuestiones que norman su funcionamiento:
• La fundamentación de esta propuesta se sustenta en la notación de base diez.
• El círculo mayor está relacionado con el concepto de cero, no como ausencia de cantidad sino más bien como enlace que permite pasar de unidades a decenas, de decena a centenas, de centenas a unidades de mil u otros similares.
• Las columnas ubicadas debajo del círculo mayor permiten representar las unidades, decenas, centenas y unidades de mil, mismas que constituirán el orden de los elementos presentes, comenzando desde la izquierda con la de menor orden, las unidades, luego las de orden mayor, decenas, centenas y unidades de mil, pudiendo ampliarse con otras columnas que permitan representación de números mayores.
• La ubicación de las respectivas cantidades de unidades, decenas, centenas y unidades de mil se llenarán de abajo hacia arriba.
• Las cantidades se representarán únicamente en la zona de los círculos pequeños, teniendo en cuenta la descomposición de cualquier número en unidades, decenas, centenas y unidades de mil.
• En la concavidad mayor, de forma temporal se ubicarán elementos únicamente durante el proceso de las operaciones, más siempre estará vacío cuando se represente una operación o cuando se presente un resultado.
• Se escogerá un tipo de grano para unidades, otro tipo para decenas, otro tipo para centenas y otro tipo para unidades de mil, acuerdo que debe estar claramente establecido y aceptado de forma que no permita confusión alguna.
• Cada tipo de grano o símbolo se ubicará únicamente en su respectiva columna de la taptana; solamente en la concavidad mayor puede ubicarse cualquier símbolo temporalmente, ya que será remplazado junto a los de la columna respectiva, con un elemento de la columna de la derecha.
• Si no se ubica ningún elemento en alguna de las columnas, esto representa un cero en lo que esa columna simboliza.
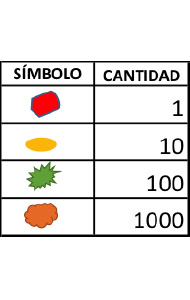
Acuerdo de simbología
Si establecemos la siguiente simbología gráfica, (en la práctica tangible, los símbolos serán distintos granos o piedritas de diferentes colores adecuadamente seleccionadas).
La siguiente semana presentaremos, la representación de una cantidad, el proceso de conteo y el algoritmo de la suma.